안녕하세요.
오늘은 B 트리 에 대해 포스팅 합니다.
B 트리 는 이진 탐색 트리의 일종으로 탐색 성능을 높이기 위해 균형있게 높이를 유지하는 균형 트리 입니다.
균형 이진 탐색 트리는 대표적으로 RedBlackTree, AVL 트리 같은것이 있습니다. 두 트리가 독특한 규칙으로 높이를 유지 하는것처럼 B 트리도 자신만의 규칙이 존재합니다.
특이한점은, 이진 트리가 아니라는 점 입니다. 규칙에 따라 노드의 자식 노드 개수는 2개 이상이 될 수 도 있습니다.
B 트리 장점
B 트리의 장점은 크게 3가지가 존재합니다.
- 균형 트리
- 데이터 로드 효율성
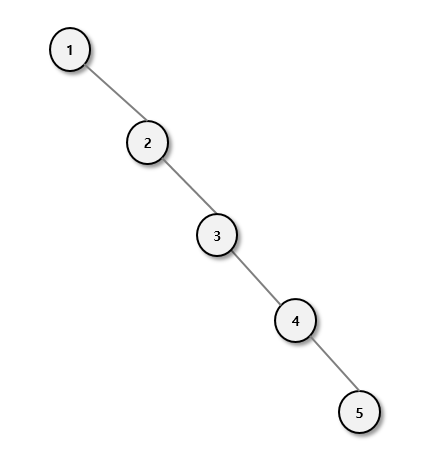
균형 트리의 장점은 이진 탐색 트리 에서도 살펴봤다시피, 노드들이 한쪽으로 치우쳐 연결 리스트의 형태가 되는것을 방지하여 검색 효율을 높일 수 있다는 장점이 있습니다.
데이터 로드 효율성 측면은 대량의 데이터로 트리를 구성할 때, 진가를 발휘합니다.
데이터가 많은경우 메모리에 트리 구조를 유지하기 보다는 외부장치에 데이터를 저장해야 합니다. 각 노드의 값을 파일로 저장한 후, 파일 정보만 저장하고 있다면 메모리에서도 충분히 트리를 유지할 수 있게 됩니다.
외부장치에서 데이터를 읽어올때 데이터가 크던 작던 블럭 크기 만큼 읽어옵니다. 즉 노드의 데이터를 특정 블럭 크기 만큼 지정하여 저장 할 수 있다면 효율적으로 데이터를 읽어올 수 있다는 장점이 생깁니다.
B 트리 구성 방법
B 트리 만의 독특한 구성 규칙이 존재합니다. 이해를 위해서 모든 규칙은 맨 마지막에 정리하고, 중요한 조건순으로 차근차근 알아가봅시다.
N차 B 트리
B 트리를 구성할 때, 가장 중요한 조건은 노드가 최대 몇개의 데이터를 가질 수 있느냐 입니다.
만약 최대 3개의 자료를 가질 수 있다고 정의하면, 노드 자식 개수는 최대 4개를 가질 수 있습니다. 이때 최대 자식 개수를 사용하여 4차 B 트리 라고 표현 합니다.
즉 일반화 해본다면, 하나의 노드가 최대 M개의 자료를 가질 수 있다면 최대 자식 노드 개수는 M+1이 되므로 M+1차 B 트리 입니다.
왜 최대 자식 노드 개수가 M+1 이냐구요? 아래 B 트리 삽입 에서 살펴봅시다!
N차 B 트리는 노드의 최대 자료수는 N-1 이며, 최대 N개의 자식노드를 가질 수 있습니다.
B 트리 탐색
B 트리 탐색은 탐색 노드와 특징을 이용합니다.
특정 노드의 범위 위치를 찾은 후 아래의 자식 노드로 이동합니다.
아래의 과정은 0016 값을 찾는 과정입니다.
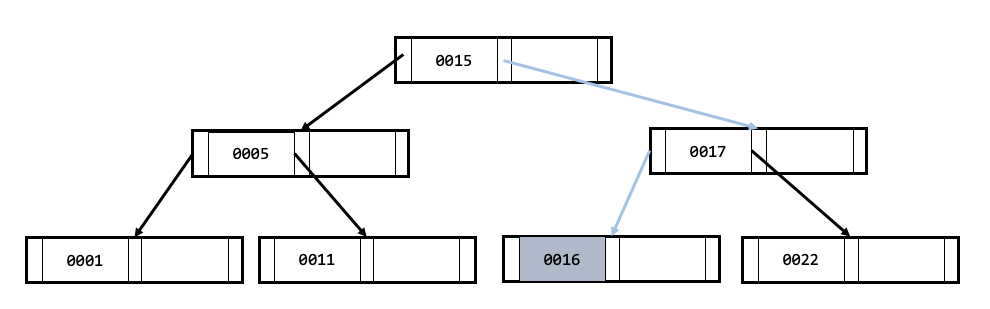
- 루트 노드에서 0016 값의 범위 위치를 찾습니다. (0015 < 0016)
- 다음 노드에 0016 값이 존재하는지 찾아봅니다. 존재하지 않으므로 0016 값의 범위 위치를 찾습니다. (0016 < 0017)
- 다음 노드는 리프노드 이므로 해당 노드에 값이 존재하지 않는다면 트리에 값이 존재하지 않음을 알 수 있습니다. 0016 값이 있으므로 탐색을 종료합니다.
B 트리 삽입
B 트리의 차수를 정할 때 홀수냐 짝수냐에 따라 알고리즘이 조금 다릅니다. 홀수가 조금 더 계산하기 편하므로 홀수로 설명하겠습니다.
3차 B 트리 를 예시로 들어봅시다. (노드의 최대 자료 개수는 2개)
삽입의 핵심은 노드 분열 작업 입니다.
아래의 삽입 과정은 최초 노드 분열이 발생하는 과정입니다.
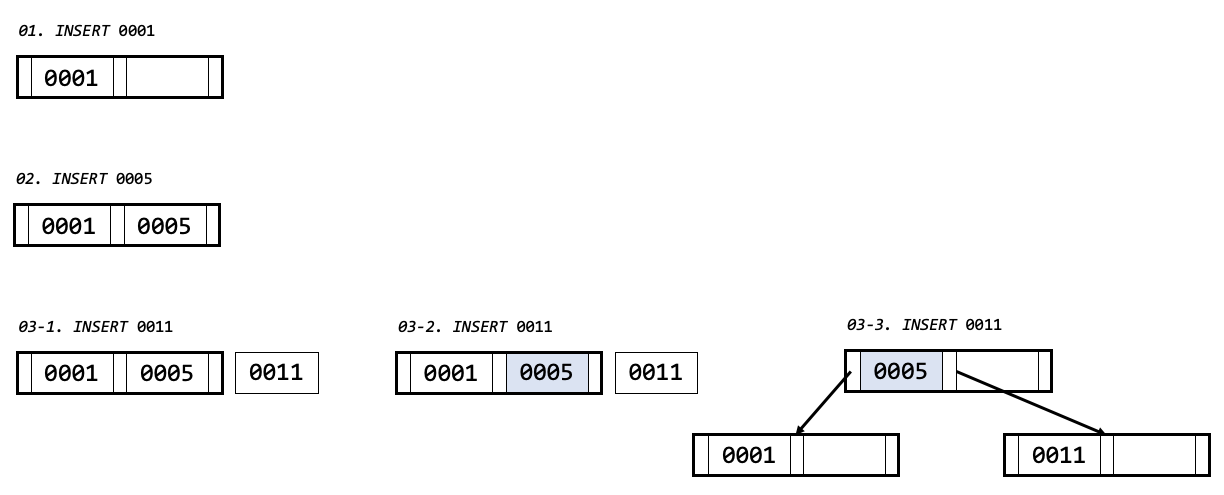
- 01~02 번 삽입 과정은 루트 노드에 빈자리가 존재하여 자리를 찾아 삽입 합니다.
- 데이터 저장 순서는 오름 차순으로 저장합니다.
- 03번은 0011 을 루트 노드에 넣을 자리가 없는 경우 입니다.
- 이때
B 트리핵심 과정 중 하나인 노드 분열이 발생합니다.
- 03-2. 루트 노드의 값들과 넣을 값을 포함하여 중간 값을 찾습니다. (홀수 차수를 고른것이 이때 편합니다.)
- 03-3. 중간 값 0005 값을 부모 노드로 올리고, 왼쪽 값들과 오른쪽 값들을 자식 노드로 각각 구성하여 연결합니다.
- 이때
아래의 과정에서 발생하는 노드 분열도 한번 살펴보시죠.
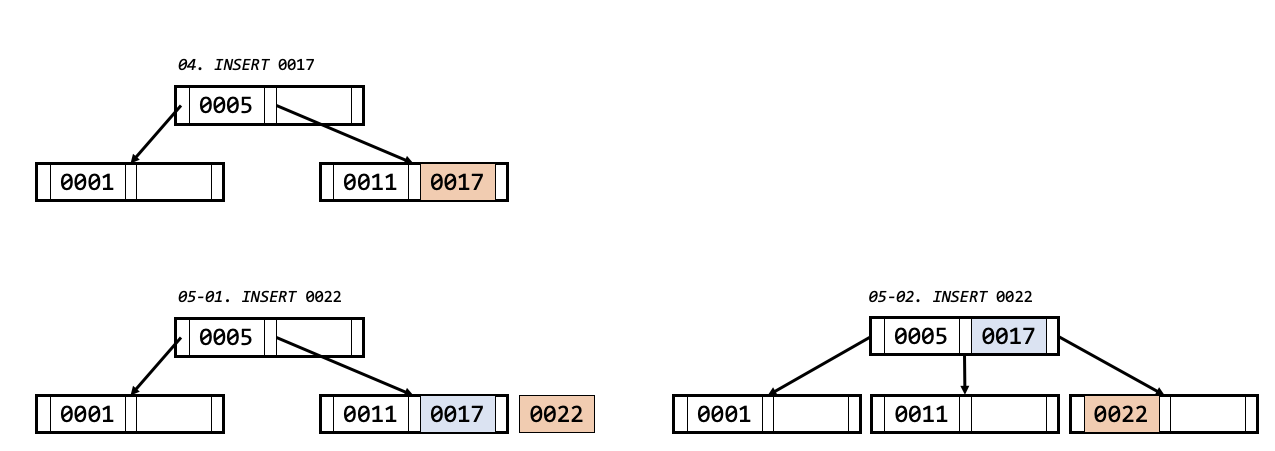
- 04번 삽입은 탐색 노드 특징을 이용하여 리프노드 까지 도달합니다.
- 리프노드에 자리가 비었으므로, 0017값이 그대로 저장됩니다.
- 05-01. 0022 값의 자리를 탐색하여 리프 노드 까지 도달했습니다.
- 05-01. 하지만, 리프 노드엔 자리가 없습니다. 노드 분열과 마찬 가지로 중간 값을 찾습니다.
- 05-02. 중간 값을 부모 노드로 이동시킵니다. (노드 분열이 발생합니다.)
- 05-02. 남은 값들은 각각 노드로 구성하여 중간 값 왼쪽, 오른쪽 자식노드로 연결합니다.
위 예시와 같이 리프노드에 공간이 부족할 때, 부모 노드로 중간 값을 옮기는 노드 분열를 수행하면 재밌는 특징이 생깁니다.
- 규칙1. 노드의 자료가 최대 N개 라면, 해당 노드의 자식 노드 개수는 항상 N+1 입니다.
- 규칙2. 모든 리프 노드들은 항상 같은 레벨에 위치하게 됩니다.
- 규칙3. 노드의 자료가 최대 N개 라면, 리프 노드가 분열 할때 항상 중간 값으로 분열 하므로 노드의 자료 개수는 [N/2]~N개가 보장 됩니다.
[3/2] ⇒ 2 (올림연산 입니다.)
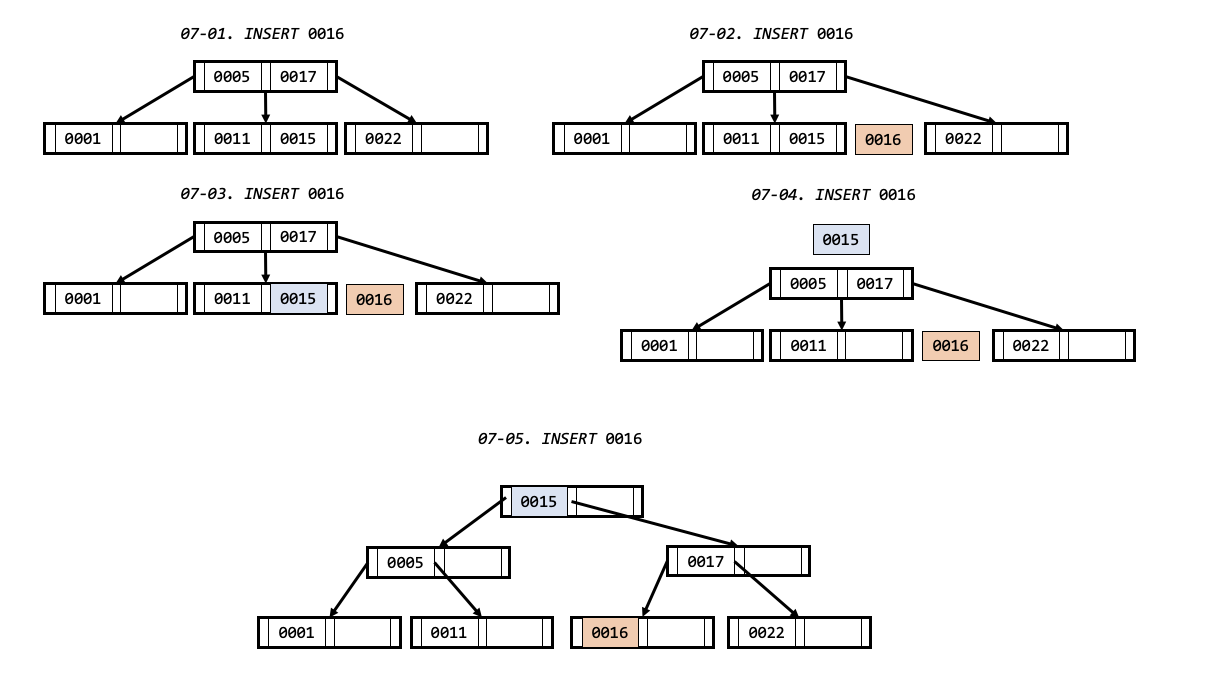
마지막으로 아래의 노드 분열을 이해 하실 수 있다면, 트리 삽입 과정을 이해 하실 수 있습니다.
B 트리 삭제
B 트리의 삭제는 크게 두가지 케이스로 나누어 생각 해볼 수 있습니다.
- 리프 노드에서 값 삭제.
- 리프 노드가 아닌 중간 노드에서 값 삭제.
리프 노드에서 삭제
이 경우에도 크게 3가지 경우로 나뉩니다.
- 리프 노드에서 값을 삭제 하더라도 최소 유지 개수 ([N/2]) 조건에 만족하는 경우.
- 리프 노드에서 값을 삭제 할 때, 최소 유지 개수를 만족하지 못하지만 바로 옆 형제 노드들 중 최소 유지 개수 보다 많아 값을 빌려올 수 있는 경우.
- 리프 노드에서 값을 삭제 할 때, 최소 유지 개수를 만족하지 못하고 옆 형제 노드들도 최소 유지 개수만 가지고 있어 값을 빌려올 수 없는 경우.
리프 노드에서 바로 삭제.
리프 노드가 최소 유지 개수를 만족하는 경우 바로 삭제가 가능합니다.
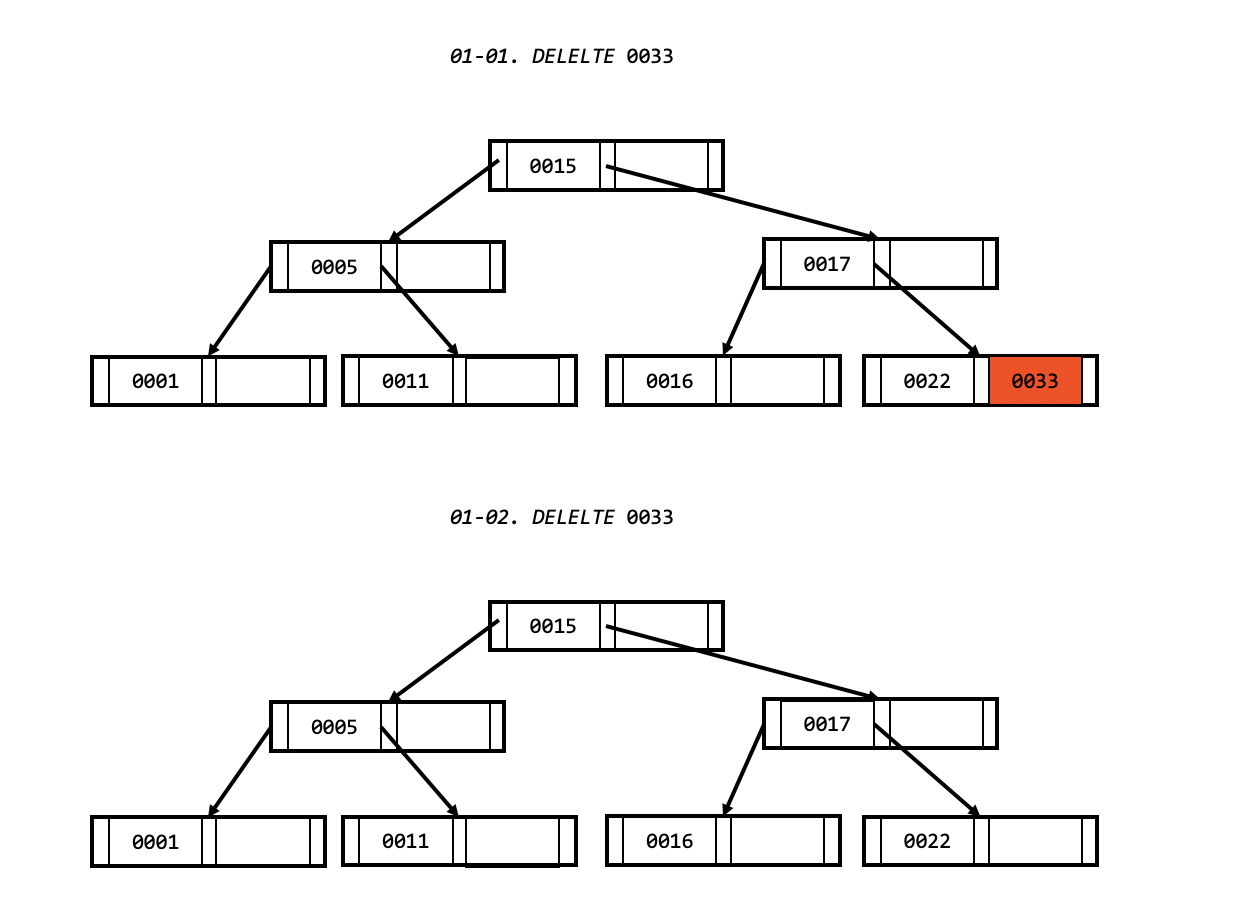
형제 노드에서 값을 빌려 오는 경우.
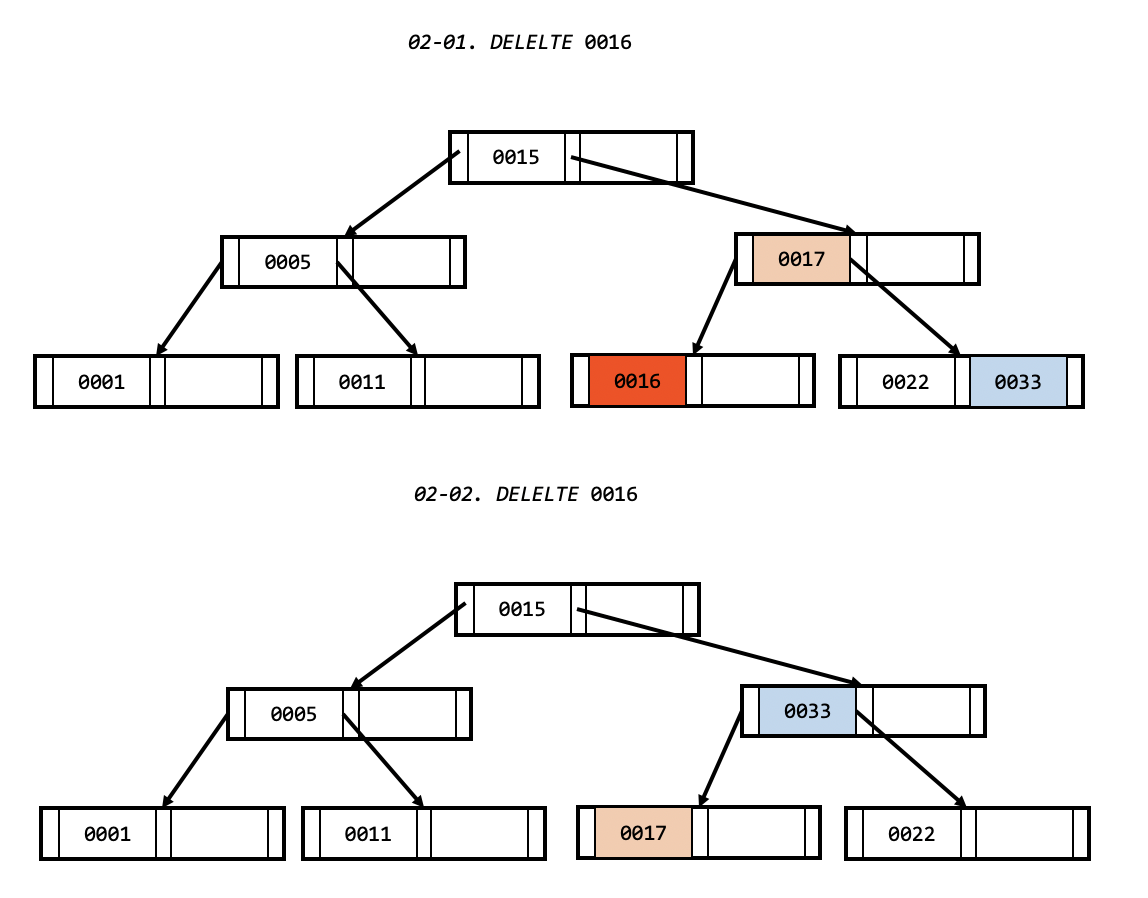
- 리프 노드의 형제 노드에서 빌려야 할 값을 찾습니다.
- 오른쪽 형제 노드라면 형제 노드중 최대값.
- 왼쪽 형제 노드라면 형제 노드중 최소 값.
- 리프 노드의 부모 노드에서 리프 노드와 형제 노드를 동시에 가리키고 있는 값을 찾습니다.
- 리프 노드에서 값을 삭제 후, 부모 노드에서 찾은 값을 리프노드로 내려주고 빌린 형제 노드 값을 부모 노드 찾은 값 자리에 넣습니다.
형제 노드에서도 값을 빌릴 수 없는 경우.
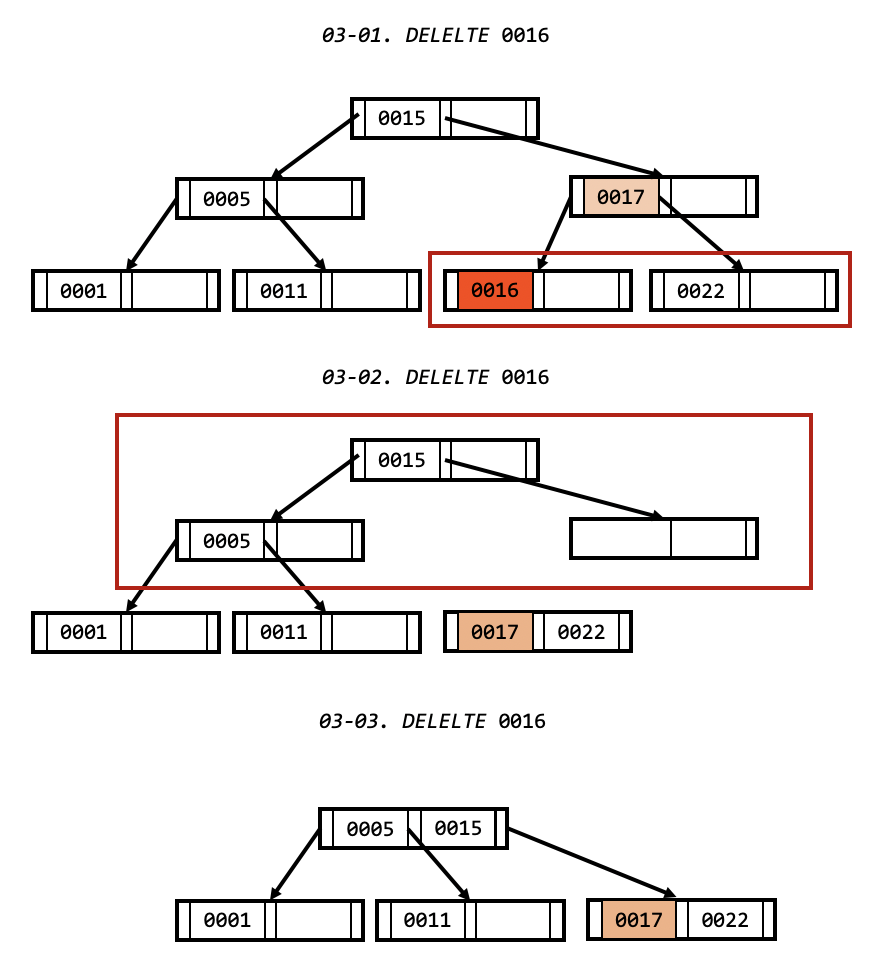
- 삭제할 리프 노드와 형제 노드를 병합 합니다. 병합 노드도 최소 개수 조건을 만족 시키기 위해 부모 노드에서 값 하나를 내려줍니다.
- 부모 노드도 최소 개수 조건을 만족하지 않는다면, 1번 과정을 리프 노드 대신 부모 노드로 치환하여 수행합니다.
- 만약 병합된 노드가 최대 개수를 넘는다면, 중간 값을 찾아 병합 노드의 부모 노드로 값을 넘겨줍니다.
중간 노드에서 삭제
해당 경우도 3가지로 나눌 수 있습니다.
- 최소 개수 보다 많아 값을 빌려올 수 있는 자식 노드가 존재하는 경우.
- 여유있는 자식 노드가 없지만, 부모 노드가 최소 개수보다 많은 경우.
- 자식 노드도, 부모 노드도 여유가 없는 경우.
자식 노드에게 값을 빌려오는 경우.
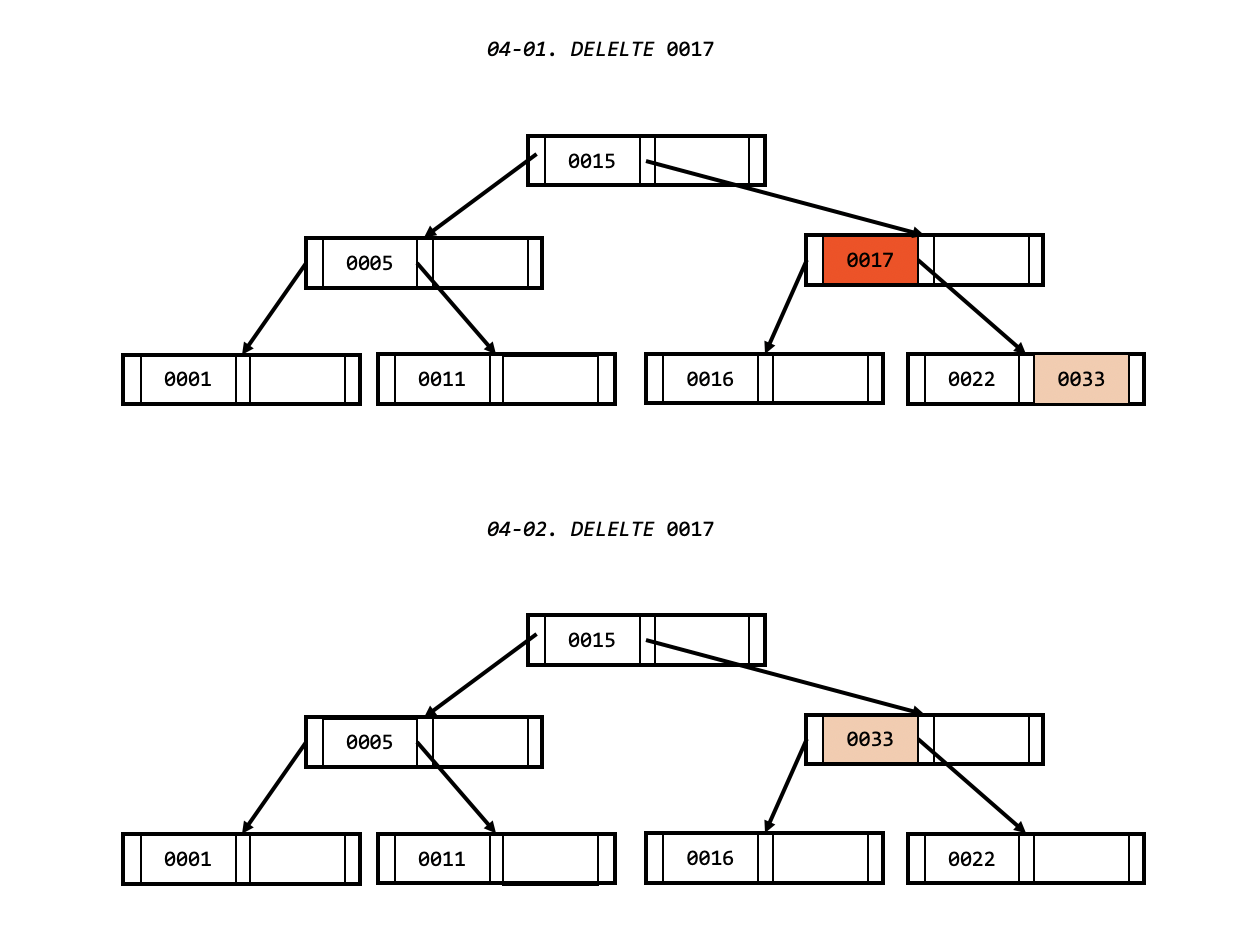
- 값을 빌려올 자식 노드의 값을 찾습니다.
- 왼쪽 자식 노드라면 최소 값을 찾습니다.
- 오른쪽 자식 노드라면 최대 값을 찾습니다.
- 타겟 노드의 값을 지우고, 해당 자리를 찾은 자식 노드의 값으로 대체 합니다.
여유있는 자식 노드는 없지만, 부모 노드가 여유가 있는 경우.
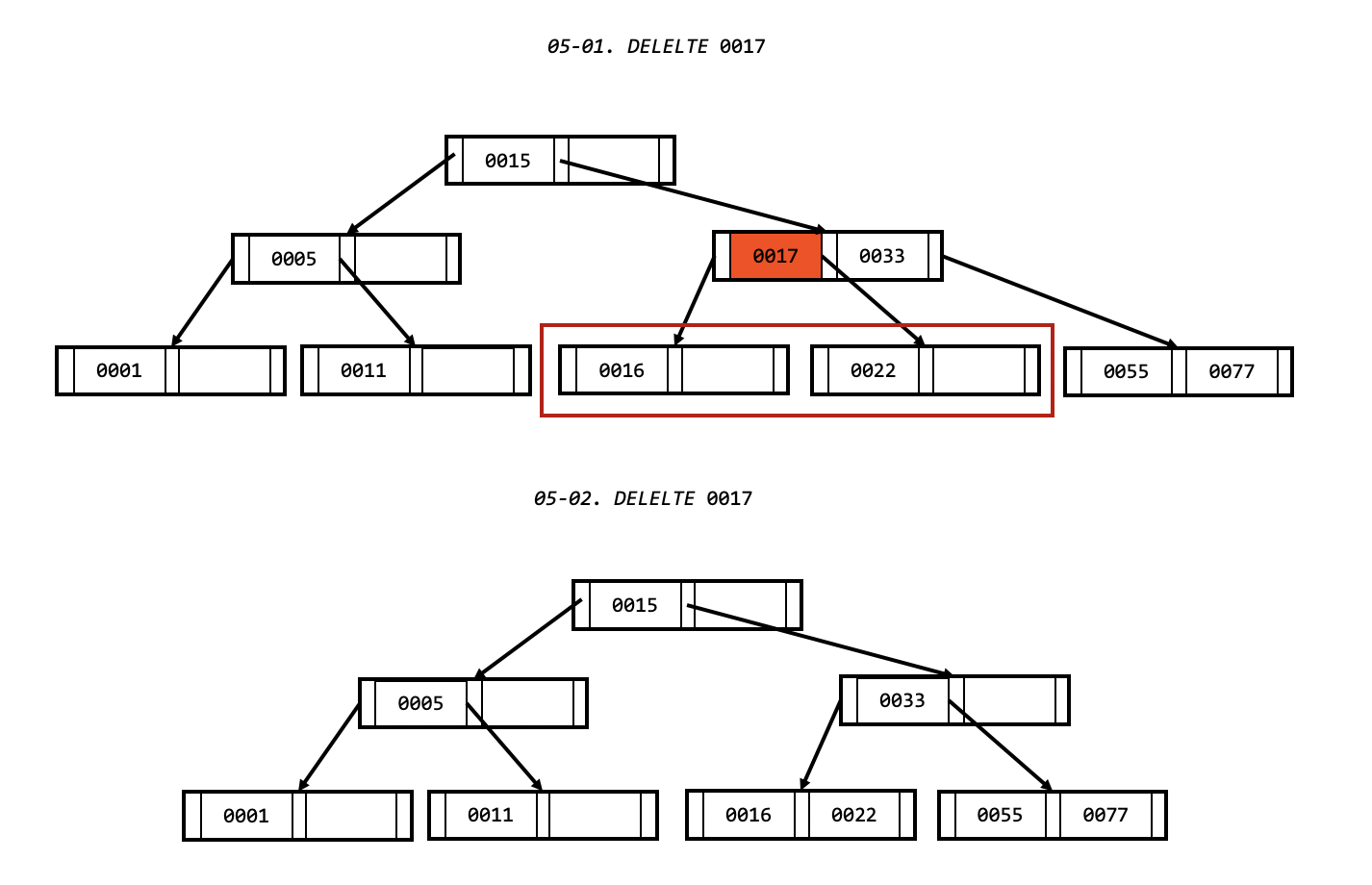
- 노드의 삭제 값의 자식 노드들을 합병합니다.
자식노드, 부모노드 둘다 여유가 없는 경우.
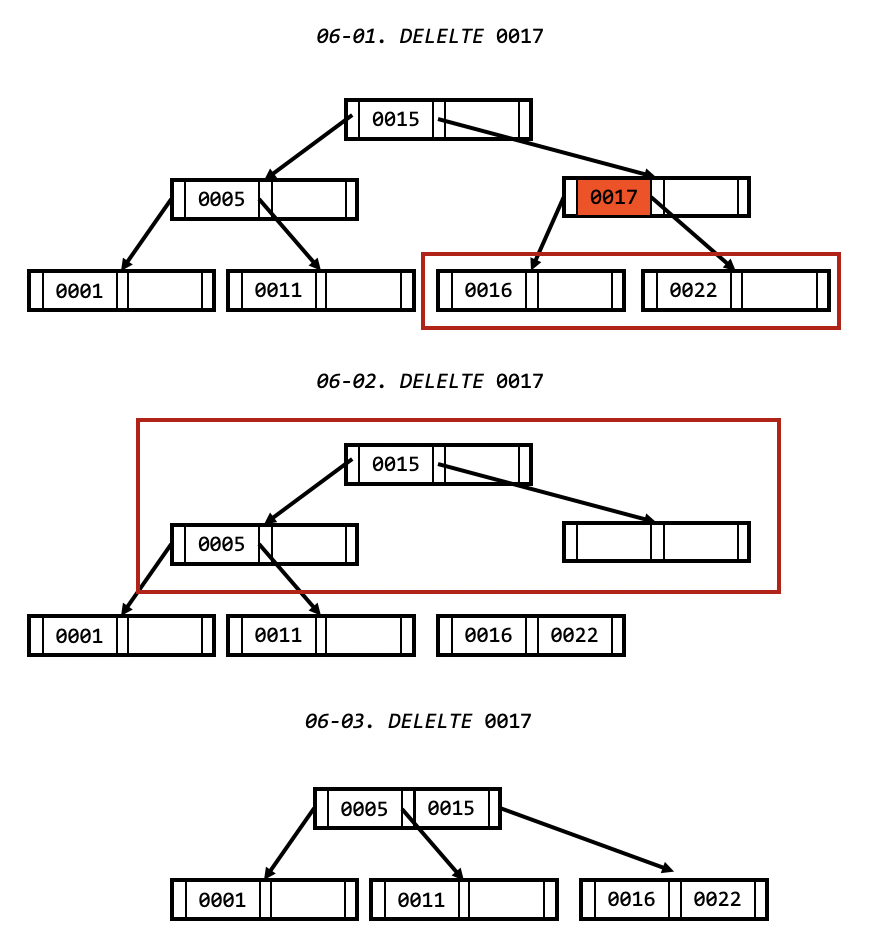
- 노드의 삭제 값의 자식 노드들을 병합합니다.
- 노드의 형제 노드와 부모노드를 대상으로 병합을 진행합니다.
- 만약 병합 노드가 최대 개수를 초과 한다면 중간 값을 추출해 병합 노드의 부모노드로 이동시킵니다.
B+트리
B 트리의 단점은 순회?
Warning!! 주관적인 생각이 섞여 있습니다.
B 트리 는 자료 순회가 단점이라는 글이 많습니다. B 트리도 트리 구조이기 때문에 트리 순회와 똑같은 시간복잡도가 걸립니다. 그렇기에 단점이라 할 수는 없습니다.
많은 자료들이 단점이라 오해(?)하는 이유는 트리 순회를 개선한 B+트리의 존재 유무 때문이 아닐까 생각이 듭니다.
리프 노드들을 모든 노드의 값이 포함되도록 처리
B+ 트리의 순회 연산의 개선 포인트는 리프 노드들의 구조에 있습니다.
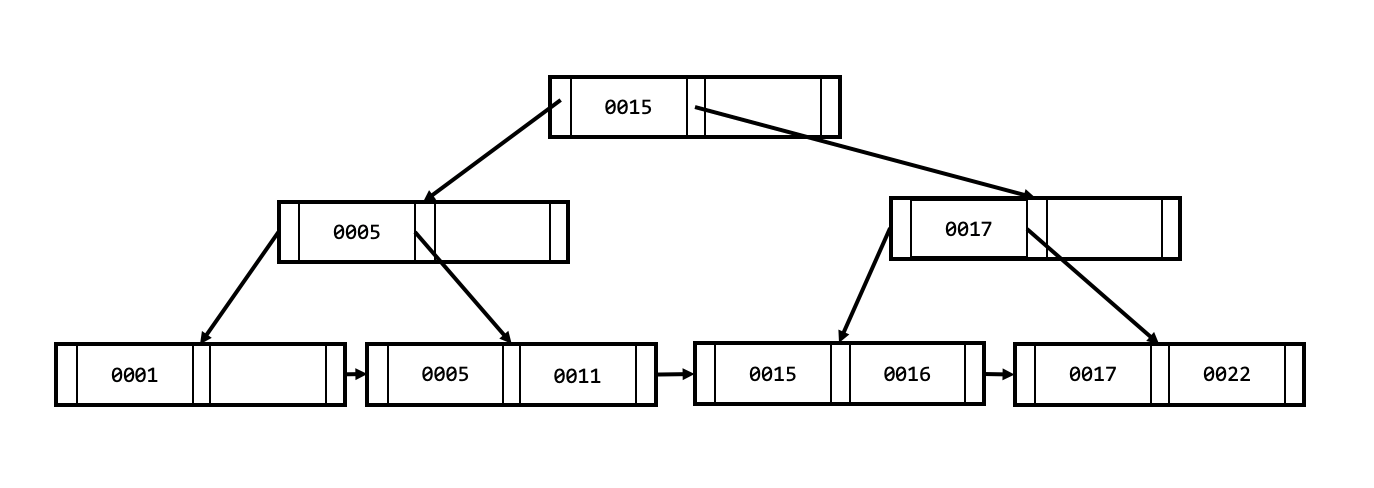
다음의 예시를 보면, 리프 노드들은 모든 값들을 포함하고 있고 연결리스트 형태를 구성하고 있습니다.
리프 노드의 위 노드들은 검색을 위해 유지하고 있는 모습입니다.
특정 범위를 순회하고 싶다면, 손쉽게 특정 리프 노드에서 차례대로 순회 할 수 있습니다.
빠른 검색-삽입-삭제 + 범위 검색 이 필요한 관계형 데이터베이스가 해당 자료구조를 사용하고 있습니다.
B 트리의 삽입, 삭제 과정을 단번에 이해하긴 어려운거 같습니다.
더군다나 트리의 특정 스냅샷 기준으로 설명했기 때문에 높이가 큰 트리인 경우에는 설명한 개념에 더해 재귀 개념 까지 합산하여 이해를 해야 하기 때문에 더 어려운거 같습니다.
B 트리 특징들을 살펴보면서 항상 만족했던 조건들을 다시 정리해보면 아래와 같습니다.
- N차 B 트리는 노드의 최대 자료수는 N-1 이며, 자식노드는 최대 N개.
- 노드의 자료가 최대 N개 라면, 해당 노드의 자식 노드 개수는 항상 N+1.
- 노드의 자료가 최대 N개 라면, 노드의 자료 개수는 [N/2] ~ N개. (루트 노드 제외)
- 모든 리프 노드들은 항상 같은 레벨에 위치한다.
오늘 준비한 포스팅은 여기까지 입니다.
읽어주셔서 감사합니다.
'자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색트리 (1) | 2021.07.12 |
|---|---|
| [자료구조] 트리(Tree) (0) | 2021.07.10 |
포스팅이 도움 되셨다면, 커피 한잔 후원해주세요!
더 좋은 포스팅 작성에 큰 힘이 됩니다.
 Buy me a coffee
Buy me a coffee